Koordinat Polar
Dalam beberapa hal, lebih mudah mencari lokasi/posisi suatu titik dengan menggunakan koordinat polar. Koordinat polar menunjukkan posisi relatif terhadap titik kutub O dan sumbu polar (ray) yang diberikan dan berpangkal pada O.
O (the pole)
ray (polar axis)
Titik P dengan koordinat polar (r, q) berarti berada diposisi:
- q derajat dari sumbu-x (sb. polar)
(q diukur berlawanan arah jarum-jam)
- berjarak sejauh r dari titik asal kutub O.
Perhatian:
jika r <>
r: koordinat radial
q: koordinat sudut
Setiap titik mempunyai lebih dari satu representasi dalam koordinat polar
(r, q) = (- r, q + np ), untuk n bil. bulat ganjil
= ( r, q + np ) , untuk n bil. bulat genap
Persamaan2 dalam Koordinat Polar
Pers. polar dari lingkaran berjari-jari a: r = a
Untuk lingkaran berjari a,
- berpusat di (0,a): r = 2a sin q
- berpusat di (a,0): r = 2a cos q
r = 2 sin q
Vektor posisi, kecepatan dan percepatan
1. Gerakan Partikel dalam bidang XY dinyatakan oleh X=10+12t-20t2 dan Y=25+15t+30t2. XY dalam meter dan t dalam detik.ditanyakan:
a. Hitung nilai dari Xo Yo Vox dan Voy
b. Hitung besar dan arah kecepatan awal Vo
c. Hitung Aox dan Aoy
A:
Mengubah persamaan posisi menjadi percepatan
A :
Jika posisi benda dinyatakan dalam persamaan dengan variable waktu, maka persamaan posisi tersebut kita turunkan (diferensialkan) menjadi persamaan kecepatan.
Gerak Lurus Beraturan (GLB)
Gerak lurus beraturan (GLB) adalah gerak benda dalam lintasan garis lurus dengan kecepatan tetap. Untuk lebih memahaminya, amati grafik berikut!

Gambar 1.7: Grafik v - t untuk GLB.
Grafik di atas menyatakan hubungan antara kecepatan (v) dan waktu tempuh (t) suatu benda yang bergerak lurus. Berdasarkan grafik tersebut cobalah Anda tentukan berapa besar kecepatan benda pada saat t = 0 s, t = 1 s, t = 2 s, t = 3 s?
Ya!, Anda benar! Tampak dari grafik pada gambar 6, kecepatan benda sama dari waktu ke waktu yakni 5 m/s.
Semua benda yang bergerak lurus beraturan akan memiliki grafik v - t yang bentuknya seperti gambar 6 itu. Sekarang, dapatkah Anda menghitung berapa jarak yang ditempuh oleh benda dalam waktu 3 s?
Anda dapat menghitung jarak yang ditempuh oleh benda dengan cara menghitung luas daerah di bawah kurva bila diketahui grafik (v-t)

Gambar 1.8: Menentukan jarak dengan menghitung luas di bawah kurva.
| Jarak yang ditempuh = luas daerah yang diarsir pada grafik v - t. |
| Cara menghitung jarak pada GLB. |
Tentu saja satuan jarak adalah satuan panjang, bukan satuan luas. Berdasarkan gambar 1.7 di atas, jarak yang ditempuh benda = 15 m.
Cara lain menghitung jarak tempuh adalah dengan menggunakan persamaan GLB. Telah Anda ketahui bahwa kecepatan pada GLB dirumuskan:

atau
s = v . t (Persamaan GLB)
Keterangan:
s = jarak tempuh (m)
v = kecepatan (m/s)
t = waktu tempuh (s)
| Dari gambar 1.8, | v = 5 m/s, sedangkan t = 3 s, sehingga jarak |
Persamaan GLB di atas, berlaku bila gerak benda memenuhi grafik seperti pada gambar 1.8. Pada grafik tersebut terlihat bahwa pada saat t = 0 s, maka v = 0. Artinya, pada mulanya benda diam, baru kemudian bergerak dengan kecepatan 5 m/s. Padahal dapat saja terjadi bahwa saat awal kita amati benda sudah dalam keadaan bergerak, sehingga benda telah memiliki posisi awal so. Untuk keadaan ini, maka persamaan GLB sedikit mengalami perubahan menjadi,
| Persamaan GLB untuk benda yang sudah bergerak sejak awal pengamatan. |
Dengan so menyatakan posisi awal benda dalam satuan meter. Kita akan kembali ke sini setelah Anda ikuti uraian berikut.
Di samping grafik v - t di atas, pada gerak lurus terdapat juga grafik s-t, yakni grafik yang menyatakan hubungan antara jarak tempuh (s) dan waktu tempuh (t) seperti pada gambar 1.9 di bawah.

Gambar 1.9: Grafik s- t untuk GLB
Perhatikan gambar 1.9 di atas. Pada saat t = 0 s, jarak yang ditempuh oleh benda s = 0, pada saat t = 1 s, jarak yang ditempuh oleh benda s = 2 m, pada saat t = 2 s, jarak s = 4 m, pada saat t = 3 s, jarak s = 6 s dan seterusnya. Berdasarkan hal ini dapat kita simpulkan bahwa benda yang diwakili oleh grafik s - t pada gambar 9 di atas, bergerak dengan kecepatan tetap 2 m/s (Ingat, kecepatan adalah jarak dibagi waktu).
Berdasarkan gambar 1.9, kita dapat meramalkan jarak yang ditempuh benda dalam waktu tertentu di luar waktu yang tertera pada grafik. Cobalah Anda lakukan hal itu dengan cara mengisi tabel di bawah.
Tabel 1: Hubungan jarak (s) dan (t) pada GLB
![]()
| 1. | Sebuah mobil bergerak dengan kecepatan tetap 36 km/jam. Berapa meterkah jarak yang ditempuh mobil itu setelah bergerak 10 menit? |
Penyelesaian:
Anda ubah dulu satuan-satuan dari besaran yang diketahui ke dalam sistem satuan SI.
t = 10 menit = 10 x 60 s = 600 s
s = v.t = 10 x 600 = 6.000 m = 6 km
Kini, kita kembali kepada apa yang telah kita bicarakan sebelum kita membahas Grafik s - t untuk GLB ini. Untuk itu kita butuh contoh.
Contoh:
| 2. | Gerak sebuah benda yang melakukan GLB diwakili oleh grafik s - t di bawah. Berdasarkan grafik tersebut, hitunglah jarak yang ditempuh oleh benda itu dalam waktu: a. 3 s b. 10 s |

Gambar 1.10: Grafik s - t untuk GLB dengan posisi awal s0.
Gambar 1.10 di atas sebenarnya menyatakan sebuah benda yang melakukan GLB yang memiliki posisi awal so. Dari grafik tersebut kita dapat membaca kecepatan benda yakni v = 4 m/s.
Seperti telah dibicarakan, hal ini berarti bahwa pada saat awal kita mengamati benda telah bergerak dan menempuh jarak sejauh so=2 m.
Jadi untuk menyelesaikan soal ini, kita akan gunakan persamaan GLB untuk benda yang sudah bergerak sejak awal pengamatan.
Penyelesaian:
Diketahui:
so = 2 m
v = 4 m/s
Ditanya:
a. Jarak yang ditempuh benda pada saat t = 3 s.
b. Jarak yang ditempuh benda pada saat t = 10 s.
Jawab:
| a. | s (t) s (3s) | = so + v.t = 2 + 4 x 3 = 14 m |
| b. | s (t) s (10s) | = so + v.t = 2 + 4 x 10 = 42 m |
Ticker Timer
Ticker timer atau mengetik waktu, biasa digunakan di laboratorium fisika untuk menyelidiki gerak suatu benda (Gambar 11.a). Pita ketik pada ticker timer merekam lintasan benda yang bergerak misalnya mobil mainan bertenaga bataerai (Gambar 11.b) berupa serangkaian titik-titik hitam disebut dot pada pita tersebut (Gambar 12). Jarak antara dot tersebut menggambarkan kecepatan gerak benda (Gambar 13). Selain itu pita ketik pada ticker time juga dapat menunjukkan apakah gerak suatu benda itu dipercepat, diperlambat atau justru bergerak dengan kecepatan tetap (Gambar 14).
(a) | (b) |
| Gambar 1.11 | (a) Ticker Ticker timer atau mengetik waktu. Pita berwarna putih adalah pita ketiknya (b). Mobil mainan bertenaga baterai untuk percobaan gerak lurus. |
![]()
Gambar 1.12: Rekaman gerak benda pada pita ketik ticker timer

Gambar 1.13: Kecepatan benda lebih besar pada gambar (a)
dibandingkan pada gambar (b)

Gambar 1.14: gerak benda (a) dipercepat (b) diperlambar (c) kecepatan tetap
Interval waktu antara dua dot terdekat atau pada pita ketik sebuah ticker timer selalu tetap, yaitu 1/50 sekon atau 0,02 s. Berdasarkan hal ini kita dapat menentukan kelajuan atau besar kecepatan rata-rata suatu benda. Langkah-langkahnya sebagai berikut. Pertama, ambil rekaman pita ketik suatu benda yang ingin kita selidiki kecepatan rata-ratanya. Guntunglah pita ketik tersebut untuk sebelas dot berturut-turut (Gambar 15). Jarak dari dot pertama sampai dot kesebelas ditempuh dalam waktu 10 x 0,02 s = 0,2 s.

Gambar 1.15: Pita ketik ticker timer:
Jarak dari dot pertama sampai dot kesebelas ditempuh dalam waktu 0,2 s.
Selanjutnya, dengan menggunakan penggaris mm kita ukur jarak dari dot pertama sampai dot kesebelas pada pita ketik. Besar keceptan rata-rata benda adalah besar jarak dibagi 0,2 s.
Konsepsi Gerak Lurus Berubah Beraturan (GLBB)Gerak lurus berubah beraturan (GLBB) adalah gerak benda dalam lintasan garis lurus dengan percepatan tetap. Jadi, ciri utama GLBB adalah bahwa dari waktu ke waktu kecepatan benda berubah, semakin lama semakin cepat. Dengan kata lain gerak benda dipercepat. Namun demikian, GLBB juga dapat berarti bahwa dari waktu ke waktu kecepatan benda berubah, semakin lambat hingga akhirnya berhenti. Dalam hal ini benda mengalami perlambatan tetap. Dalam modul ini, kita tidak menggunakan istilah perlambatan untuk gerak benda diperlambat. Kita tetap saja menamakannya percepatan, hanya saja nilainya negatif. Jadi perlambatan sama dengan percepatan negatif.
Contoh sehari-hari GLBB adalah peristiwa jatuh bebas. Benda jatuh dari ketinggian tertentu di atas. Semakin lama benda bergerak semakin cepat.
Kini, perhatikanlah gambar 2.1 di bawah yang menyatakan hubungan antara kecepatan (v) dan waktu (t) sebuah benda yang bergerak lurus berubah beraturan dipercepat.

Gambar 2.1: Grafik v - t untuk GLBB dipercepat.
Besar percepatan benda,
![]()
dalam hal ini,
v1 = vo
v2 = vt
t1 = 0
t2 = t
sehingga,
![]()
atau
a.t = vt - vo
kita dapatkan,
| Persamaan kecepatan GLBB |
vo = kecepatan awal (m/s)
vt = kecepatan akhir (m/s)
a = percepatan ()
t = selang waktu (s)
Perhatikan bahwa selama selang waktu t (pada kegiatan lalu kita beri simbol Dt), kecepatan benda berubah dari vo menjadi vt sehingga kecepatan rata-rata benda dapat dituliskan:
karena |
|
Kita tahu bahwa kecepatan rata-rata
| , maka |
![]()
atau
| Persamaan jarak GLBB |
s vo a t | = jarak yang ditempuh = kecepatan awal (m/s) = percepatan ( = selang waktu (s) |
Bagaimana? Dapat diikuti? Ulangi lagi penalaran di atas agar Anda benar-benar memahaminya. Bila sudah, mari kita lanjutkan!
Bila dua persamaan GLBB di atas kita gabungkan, maka kita akan dapatkan persamaan GLBB yang ketiga (kali ini kita tidak lakukan penalarannya). Persamaan ketiga GLBB dapat dituliskan:
| Persamaan kecepatan sebagai fungsi jarak |
Contoh:
| 1. | Benda yang semula diam didorong sehingga bergerak dengan percepatan tetap 3 Penyelesaian: | |
| vt | = vo + a.t = 0 + 3 . 5 = 15 m/s | |
Contoh:
| 2. | Mobil yang semula bergerak lurus dengan kecepatan 5 m/s berubah menjadi 10 m/s dalam waktu 6 s. Bila mobil itu mengalami percepatan tetap, berapakah jarak yang ditempuh dalam selang waktu 4 s itu? Penyelesaian: | |
vt 10 10 - 5 a | = vo + a.t | |
Setelah dapat percepatan a, maka dapat dihitung jarak yang ditempuh mobil dalam waktu 4 s: | ||
| | |
Contoh:
| 3. | Sebuah mobil yang melaju dengan kecepatan 72 km/jam mengalami pengereman sehingga mengalami perlambatan 2 Penyelesaian: | |
0 s | = 20 = 400 - 4 s = 400 / 4 = 100 meter | |
Contoh:
| 4. | Benda yang bergerak lurus berubah beraturan diwakili oleh grafik v - t di bawah.
Tentukan: Penyelesaian: a = (6-2) / 10 a = 0,4 Jarak yang ditempuh oleh benda dalam waktu 10 s dapat kita hitung dalam 2 cara. Cara 1: | |
| = 2 . 10 + ½ . 0,4 . 10 = 20 + 20 = 40 meter | |
| ||
Contoh:
| 5. | Mobil yang bergerak GLBB diwakili oleh grafik v - t seperti pada gambar di bawah. Berapakah jarak toal yang ditempuh oleh mobil itu? Soal seperti ini agak berbeda dengan soal-soal sebelumnya. Oleh karenanya sebelum menjawab pertanyaan di atas, ada baiknya Anda perhatikan penjelasan berikut ini. Dari grafik di atas tampak selama perjalanannya, mobil mengalami 2 macam gerakan. Tiga jam pertama (dari 0 - 3 pada sumbu t) mobil bergerak dengan kecepatan tetap, yakni 30 km/jam. Ini berarti mobil menjalani gerak lurus beraturan (GLB). Dua jam berikutnya (dari 3 - 5 pada sumbu t) gerak mobil diperlambat, mula-mula bergerak dengan kecepatan awal 30 km/jam lalu berhenti. Artinya mobil menjalani gerak lurus berubah beraturan diperlambat. Jarak total yang ditempuh mobil dapat dihitung dengan menggunakan 2 cara sebagai berikut. Cara 1: Jarak yang ditempuh selama 2 jam berikutnya (GLBB) Jarak total yang ditempuh mobil: Cara 2: Jarak total = luas trapesium |
Gerak Melingkar
![]()
Pengertian Gerak Melingkar
Dalam kehidupan sehari-hari sering kita jumpai berbagai macam gerak melingkar, seperti compact disc (CD), gerak bulan mengelilingi bumi, perputaran roda ban mobil atau motor, komidi putar, dan sebagainya.
Jika kita perhatikan benda-benda tersebut pada saat bergerak, maka dikatakan benda melakukan gerak melingkar yang selama pergerakkannya berada dalam bidang datar.
Gerak Melingkar adalah gerak benda pada lintasan yang berbentuk lingkaran. Gerak melingkar sama halnya dengan gerak lurus dibagi menjadi dua : Gerak Melingkar Beraturan (GMB) dan Gerak Melingkar Berubah Beraturan (GMBB).
Gerak melingkar beraturan
Gerak Melingkar Beraturan (GMB) adalah gerak melingkar dengan besar kecepatan sudut  tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial
tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial 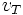 dengan jari-jari lintasan
dengan jari-jari lintasan 
Arah kecepatan linier 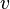 dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial
dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial 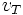 . Tetapnya nilai kecepatan
. Tetapnya nilai kecepatan 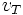 akibat konsekuensi dar tetapnya nilai
akibat konsekuensi dar tetapnya nilai  . Selain itu terdapat pula percepatan radial
. Selain itu terdapat pula percepatan radial  yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
Bila 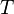 adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran
adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran  , maka dapat pula dituliskan
, maka dapat pula dituliskan
Kinematika gerak melingkar beraturan adalah
dengan  adalah sudut yang dilalui pada suatu saat
adalah sudut yang dilalui pada suatu saat 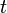 ,
,  adalah sudut mula-mula dan
adalah sudut mula-mula dan  adalah kecepatan sudut (yang tetap nilainya).
adalah kecepatan sudut (yang tetap nilainya).
Gerak melingkar berubah beraturan
Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak melingkar dengan percepatan sudut  tetap. Dalam gerak ini terdapat percepatan tangensial
tetap. Dalam gerak ini terdapat percepatan tangensial  (yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial
(yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial 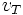 ).
).
Kinematika GMBB adalah
dengan  adalah percepatan sudut yang bernilai tetap dan
adalah percepatan sudut yang bernilai tetap dan  adalah kecepatan sudut mula-mula.
adalah kecepatan sudut mula-mula.
Turunan dan integral
Seperti halnya kembarannya dalam gerak linier, besaran-besaran gerak melingkar pun memiliki hubungan satu sama lain melalui proses integrasi dan diferensiasi.
[sunting] Hubungan antar besaran sudut dan tangensial
Antara besaran gerak linier dan melingkar terdapat suatu hubungan melalui  khusus untuk komponen tangensial, yaitu
khusus untuk komponen tangensial, yaitu
Perhatikan bahwa di sini digunakan  yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
untuk suatu selang waktu kecil atau sudut yang sempit.




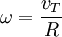








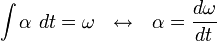
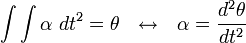


Terimakasih, sangat membantu saya...
BalasHapuswww.gusfikom.blogspot.com