Fluida Dinamika

Aliran air yang ada di alam ini memiliki bentuk yang beragam, karena berbagai sebab dari keadaan alam baik bentuk permukaan tempat mengalirnya air juga akibat arah arus yang tidak mudah untuk digambarkan. Misalnya aliran sungai yangs edang banjir, air terjun dari suatu ketinggian tertentu, dan sebagainya. Contoh yang disebutkan di bagian depan memberikan gambaran mengenai bentuk yang sulit dilukiskan secara pasti. Namun demikian, bila kita kaji secara mendalam maka dalam setiap gerakan partikel tersebut akan selalu berlaku hukum ke-2 Newton. Oleh sebab itu, agar kita labih mudah untuk memahami perilaku air yang mengalir diperlukan pemahaman yang berkaitan dengan kecepatan (laju air) dan kerapatan air dari setiap ruang dan waktu. Bertolak dari dua besaran ini aliran air akan mudah untuk dipahami gejala fisisnya, terutama dibedakan macam-macam alirannya.

Bertolak dari kecepatan sebagai fungsi dari tempat dan waktu dapat dibedakan menjadi:

a. Aliran steady (mantap) dan non steady (tidak mantap)

b. Aliran rotational dan aliran irotational

Aliran air dikatakan steady (mantap) apabila kelajuan air pada setiap titik tertentu setiap saat adalah konstan. Hal ini berarti pada titik tersebut kelajuannya akan selalu konstan. Hal ini barati pada aliran steady (mantap) kelajuan pada satu titik tertentu adalah tetap setiap saat, meskipun kelajuan aliran secara keseluruhan itu berubah/berbeda.

Aliran steady ini akan banyak dijumpai pada aliran air yang memiliki kedalaman yang cukup, atau pada aliran yang yang memiliki kecepatan yang kecil. Sebagai contoh aliran steady ini adalah aliran laminier, yakni bahwa arus air memiliki arus yang sederhana (streamline/arus tenang), kelajuan gerak yang kecil dengan dimensi vektor kecepatannya berubah secara kontinyu dari nol pada dinding dan maksimum pada sumbu pipa (dimensi linearnya kecil) dan banyak terjadi pada air yang memiliki kekentalan rendah. Selanjutnya aliran air dikatakan tidak mantap (non steady) apabila kecepatan v pada setiap tempat tertentu dan setiap saat tidak konstan. Hal ini berarti bahwa pada aliran ini kecepatan v sebagai fungsi dari waktu.

Dalam aliran ini elemen penyusun air akan selalu berusaha menggabungkan diri satu sama lain dengan elemen air di sekelilingnya meskipun aliran secara keseluruhan berlangsung dengan lancar. Contoh aliran tidak steady ini adalah aliran turbulen, yakni bahwa partikel dalam fluida mengalami perubahan kecepatan dari titik ke titik dan dari waktu ke waktu berlangsung secara tidak teratur (acak). Oleh sebab itu aliran turbulen biasanya terjadi pada kecepatan air yang tinggi dengan kekentalan yang relatif tinggi serta memiliki dimensi linear yang tinggi, sehingga terdapat kecenderungan berolak selama pengalirannya.

Di samping aliran laminier dan aliran turbulen dikenal pula aliran yang memiliki profil kecepatan datar, tetapi aliran ini hanya dikenal pada fluida yang tidak memiliki kekentalan (koefisien kekentalannya nol) dan mengalir secara lambat. Sedangkan air adalah tergolong pada fluida yang memiliki kekentalan, sehingga air tidak dapat digolongkan sebagai aliran datar.

Selanjutnya aliran irrotational adalah aliran air yang tidak diikuti perputaran partikel penyusun air tersebut, sedangkan aliran rotational adalah aliran yang diikuti perputaran partikel penyusun air. Hal ini memberikan gambaran bahwa untuk aliran rotational dapat diberikan istilah rotasi. Salah satu cara untuk mengetahui adanya aliran rotasi ini antara lain bila di permukaan air terapung sebuah tongkat yang melintang selama aliran gerak tongkat tersebut akan mengalami gerakan yang berputar di samping berpindag secara translasi akibat aliran air tersebut. Contoh aliran rotasi adalah aliran yang berupa aliran pusaran, yakni suatu aliran yang vektor kecepatannya berubah dalam arah tegak/transversal.

Selanjutnya bila ditinjau dari perubahan massa jenis air yang mengalir maka akan dikenal aliran-aliran sebagai berikut:

1. Aliran viscous dan aliran non viscous
2. Aliran termampatkan dan aliran tak termampatkan

Aliran viscous adalah aliran dengan kekentalan, atau sering disebut aliran fluida pekat. Kepekatan fluida ini tergantung pada gesekan antara beberapa partikel penyusun fluida. Di samping itu juga gesekan antara fluida itu sendiri dengan tempat terjadinya aliran tersebuut. Untuk aliran air lebih didekatkan pada aliran dengan kekentalan yang rendah, sehingga aliran air dapat berapda pada aliran non viscous.

Selanjutnya aliran termampatkan adalag aliran yang terjadi pada fluida yang selama pengalirannya dapat dimampatkan atau berubah volumenya, sehingga akan mengubah pula massa jenis fluida tersbeut. Aliran termampatkan ini pada umumnya berlangsung pada gas, sedangkan pada air alirannya lebih didekatkan pada pengertian aliran tak termampatkan yakni bahwa selama pengaliran air tersebut massa jenis air dianggap tetap besarnya.

Dari uraian yang telah dikemukakan di bagian depan, maka agar aliran air dapat dipahami dengan mudah maka aliran yang dimaksud dalam pembahasan nanti labih ditekankan pada aliran-aliran yang meliputi:

1. Aliran air merupakan aliran yang mantap

2. Aliran air merupakan aliran yang tidak berputar (irrotational = tidak berotasi)

3. Aliran air merupakan aliran yang tidak termampatkan, yakni bahwa selama pengaliran berlangsung massa jenisnya tetap

4. Aliran air merupakan merupakan aliran tanpa kekentalan (kekentalannya rendah)

Melalui pengertiannya seperti yang telah dikemukakan di atas selanjutnya akan dikenal aliran stasioner, yakni bahwa aliran air tersebut akan membentuk gas alir yang tertentu dan partikel penyusun air akan melalui jalur tertentu yang pernah dilalui oleh pertikel penyusun air di depannya.

Gambar 1. Aliran stasioner

Pada aliran stasioner tersebut garis alirnya digambarkan dalam titik P, Q, dan R. Hal ini berarti air akan lewat pada titik-titik P, selanjutnya Q dan R. Pada aliran ini di setiap titik dalam pipa tersebut (titik P, atau titik Q atau titik R) tidak bekerja gaya, dan beda tekanan pada masing-masing titik dapat ditiadakan. Oleh sebab itu kecepatan aliran air di titik tertentu adalah sama. Namun demikian kecepatan aliran pada titik P, titik Q, dan titik R dapat saja berbeda besarnya. Gambar berikut adalah gambar yang memperlihatkan arus yang streamline dan turbulen.

Gambar 2. Arus turbulen dan streamline

Garis-garis yang digambarkan dalam tabung 3 ini disebut sebagai garis alir atau garis alur. Kecepatan titik A, B, dan C akan berbeda-beda.

Bilangan Reynold merupakan besaran fisis yang tidak berdimensi. Bilangan ini dipergunakan sebagai acuan dalam membedakan aliran laminier dan turbulen di satu pihak, dan di lain pihak dapat dimanfaatkan sebagai acuan untuk mengetahui jenis-jenis aliran yang berlangsung dalam air. Hal ini didasarkan pada suatu keadaan bahwa dalam satu tabung/pipa atau dalam satu tempat mengalirnya air, sering terjadi perubahan bentuk aliran yang satu menjadi aliran yang lain. Perubahan bentuk aliran ini pada umumnya tidaklah terjadi secara tiba-tiba tetapi memerlukan waktu antara, yakni suatu waktu yang relatif pendek dengan diketahuinya kecepatan kristis dari suatu aliran. Kecepatan kritis ini pada umumnya akan dipengaruhi oleh ukuran pipa, jenis zat cair yang lewat dalam pipa tersebut.

Berdasarkan eksperimen yang telah dilakukan terdapat empat besaran yang menentukan apakah aliran tersebut digolongkan aliran laminier ataukah aliran turbulen. Keempat besaran tersebut adalah besaran massa jenis air, kecepatan aliran, kekentalan, dan diameter pipa. Kombinasi dari keempatnya akan menentukan besarnya bilangan Reynold. Oleh sebab itu, bilangan Reynold dapat dituliskan dalam keempat besaran tersebut sebagai berikut.

R_e = (ρ v D)/η

Keterangan:

R_e : bilangan Reynold

ρ : massa jenis

η : viscositas/kekentalan

v : kecepatan aliran

D : diameter pipa

Hasil perhitungan berdasarkan eksperimen didapatkan ketentuan bahwa untuk bilangan Reynold berikut ini:

0 <>e ≤ 2000, aliran disebut laminier

2000 <>e ≤ 3000, aliran disebut transisi antara laminier dan aliran turbulen

R_e > 3000, aliran turbulen

Dalam pembahasan aliran air, baik aliran air yang lewat sungai maupun melalui pipa oleh PAM, istilah debit air banyak dikenal.

Gambar 3. Aliran air lewat pipa.

Debit merupakan ukuran banyaknya volume air yang dapat lewat dalam suatu tempat atau yang dapat ditampung dalam suatu tempat tiap satu satuan waktu tertentu. Satuan debit pada umumnya mengacu pada satuan volume dan satuan waktu. Apabila Q menyatakan debit air dan v menyatakan volume air, sedangkan ∆t adalah selang waktu tertentu mengalirnya air tersebut, maka hubungan antara ketiganya dapat dinyatakan sebagai berikut:

Q = V/∆t

V : volume satuannya m³ (MKS) atau cm³ (cgs)

∆t : selang waktu tertentu satuannya second

Satuan Q adalah m³/sec (MKS) dan cm³ (cgs)

Gambar 4. Bak penampung air

Seperti telah diungkapkan di bagian depan bahwa aliran air pada umumnya berkaitan dengan kecepatan pengalirannya, dan massa jenis air itu sendiri. Aliran air dikatakan memiliki sifat ideal apabila air tersebut tidak dapat dimampatkan dan berpindah tanpa mengalami gesekan. Hal ini berarti bahwa pada gerakan air tersebut memiliki kecepatan yang tetap pada masing-masing titik dalam pipa dan geraknya beraturan akibat pengaruh gravitasi bumi di suatu tempat terhadap partikel penyusun air tersebut. Namun demikian sifat seperti yang telah diungkapkan di bagian depan tersebut dalam kehidupan sehari-hari sering sulit dijumpai dalam kenyataan, sehingga besarnya debit air yang mengalir pada sembarang aliran tersebut juga tidak mudah. Oleh sebab itu dalam pembahasan kita nanti ukuran debit didasarkan pada aliran ideal seperti yang telah diungkapkan di bagian depan.

Gambar 5. Gerak zat cair dalam tabung dari posisi (a) dan (b)

Lihat gambar di atas, suatu pipa terbuka yang luas penampang ujung kiri adalah A₁ dan mengalir air dengan kecepatan V₁, selanjutnya air mengalir melalui pipa kanan yang memiliki luas penampang A₂ dengan kecepatan pengaliran adalah V₂, maka berdasarkan sifat yang telah dikemukakan di depan akan berlaku hukum kekekalan massa, yakni bahwa selama pengaliran tidak ada fluida yang hilang, maka selama t detik akan berlaku persamaan:

A₁ V₁ g t = A₂ V₂ g t

A₁ V₁ = A₂ V₂ = konstan

Persamaan tersebut merupakan persamaan kontinuitas, dan sebagai konsekuensi aliran semacam ini adalah bahwa lecepatan pengaliran air akan terbesar pada suatu tempat yang memiliki luas penampang terkecil.

Di sini volume air yang mengalir V = A v t

Jadi selama t detik besarnya debit air yang dapat keluar adalah

Q = (A v t)/t

Q = A v

Seperti telah diungkapkan di bagian depan bahwa aliran air dalam suatu tabung akan bergantung pada tingginya permukaan air di dalam tabung tersebut dan luas penampang lubang yang terdapat dalam tabung. Hal ini berarti bahwa debit air yang mengalir dalam tabung akan bergantung pada ketinggian permukaan air dalam tabung dan luas penampangnya. Gambar di bawah ini memperlihatkan bahwa tabung dengan ketinggian permukaan air yang sama tingginya tetapi luas lubang pengaliran berbeda. Selanjutnya air dibiarkan mengalir dalam waktu yang sama.

Gambar 6. Peluapan air melalui lubang yang memiliki diameter berbeda.

Dari gambar di atas nampak jelas bahwa banyaknya air yang meluah melalui lubang tabung yang memiliki luas penampang yang lebih besar akan lebih banyak dibandingkan dengan tabung yang memiliki luas penampang yang lebih kecil. Hal ini disebabkan luas penampang lubang pengaliran air berbeda, yakni lubang yang satu lebih besar dari yang lainnya.

Selanjutnya perhatikan gambar berikut ini, di bawah ini terdapat dua tabung sama besar, diberikan dua lubang yang sama besarnya dan lubang tersebut berada pada ketinggian yang sama. Seterusnya pada tabung diisi dengan air yang berbeda tingginya dan dibiarkan air mengalir melalui lubang tersebut.

Gambar 7. Peluapan air melalui lubang sama tetapi ketinggian air berbeda.

Dari aliran air dalam selang waktu yang bersamaan akan dapat diketahui bahwa air dalam lubang tabung yang memiliki permukaan yang lebih tinggi akan memberikan gambaran debit air yang lebih besar daripada tabung yang memiliki ketinggian permukaan yang lebih rendah. Hal ini disebabkan pada permukaan air yang lebih tinggi gaya berat yang diberikan air semakin besar, sehingga memiliki kecenderungan tekanan yang lebih besar daripada tabung yang memiliki ketinggian permukaan air yang lebih rendah. Akibatnya aliran air akan lebih cepat dari yang lainnya. Dengan demikian akan memiliki debit yang lebih besar dari lainnya, semakin tinggi permukaan air dalam tabung akan semakin besar kecepatan air yang keluar dari tabung.

Fluida Statik

Pada kegiatan pertama ini dibahas mengenai fluida statik. Pada kehidupan sehari-hari, sering digunakan air sebagai contoh. Marilah kita perhatikan air tenang yang berada di tempayan.

Gambar 1. Gaya-gaya yang bekerja pada dinding tempayan

tempat fluida adalah gaya normal

Cairan yang berada dalam bejana mengalami gaya-gaya yang seimbang sehingga cairan itu tidak mengalir. Gaya dari sebelah kiri diimbangi dengan gaya dari sebelah kanan, gaya dari atas ditahan dari bawah. Cairan yang massanya M menekan dasar bejana dengan gaya sebesar Mg. Gaya ini tersebar merata pada seluruh permukaan dasar bejana sebagaimana diperhatikan oleh bagian cairan dalam kolom kecil pada gambar 2. Selama cairan itu tidak mengalir (dalam keadaan statis), pada cairan tidak ada gaya geseran sehingga hanya melakukan gaya ke bawah oleh akibat berat cairan dalam kolom tersebut:

W = m g = ρ V g (1)

di mana ρ adalah kerapatan zat cair dan V adalah volume kolom. Jika V = h ∆A, kita dapatkan:

W = ρ h ∆A g (2)

Jika berat itu ditopang oleh luasan ∆A, yang sebanding dengan luas ∆A, akibatnya gaya ini tersebar rata di permukaan dasar bejana.

Tekanan sebagai perbandingan gaya dengan luas, seperti diilustrasikan pada gambar 2.

gaya ρ h ∆A g

p = = = ρ g h (3)

luas ∆A

Di mana p adalah tekanan yang dialami dasar bejana. Dalam satuan tekanan diukur dalam N/m², dan dinamai Pascal yang disingkat Pa.

Gambar 2. Cairan setinggi h menekan dasar bejana A

Sebagai contoh, misalnya akan kita cari tekanan dalam Pa, yang dialami dasar bejana cairan dengan ρ = 670 kg/m³ dan dalamnya 46 cm.

p = ρ g h = (670 kg/m³) (9,8 m/s²) (0,46 m)

= 3020 kg.m/s² = 3020 n/m² = 3020 pa

Tekanan adalah kuantitas skalar tanpa arah. Gaya yang menghasilkan tekanan yang bekerja pada permukaan adalah vektor yang arahnya selalu tegak lurus ke permukaan. Kita dapat menggunakan keadaan setimbang gaya-gaya yang bekerja pada bagian kecil cairan, seperti dilukiskan pada gambar 3.

Gambar 3. Keseimbangan gaya pada bagian kecil cairan.

Bagian kecil cairan yang tebalnya ∆A dan luas permukaan bagian atas (ada bagian bawah) A serta luas sisi lainnya A mengalami keseimbangan gaya. Dalam hal ini cairan tidak mengalami pergolakan yang mengakibatkan cairan mengalir. Tiap bagian dari cairan mestilah diam. Tekanan yang dilakukan bagian cairan lain pada bagian kecil cairan tersebut yang dilakukan oleh gaya-gaya F₃ dan F₄ saling meniadakan, demikian pula oleh gaya-gaya F₅ dan F₆. Gaya F₂ mestilah cukup besar terhadap F₁ agar dapat menopang bagian cairan tersebut.

Karena F₃ = F₄ dan F₅ = F₆, maka p₃ (=F₃/A₂) = p₄ (=F₄/A₂) dan p₅ (=F₅/A₂) = p₆ (F₆/A₂)

Sekarang, karena F₂ > F₁, maka

p₂ A₁ . p₁ A₁ = ρ g A₁ ∆h

p₂ . p₁ = ρ g ∆h

atau

∆p = ρ g ∆h (4)

Jadi, apabila kerapatannya konstan, perubahan tekanan di antara dua titik di dalam cairan berbanding lurus dengan perbedaan kedalamannya. Pada kedalaman yang sama mempunyai tekanan yang sama. Selama variasi tekanan di dalam cairan statis hanya tergantung pada kedalamannya, maka penambahan tekanan dari luar yang dilakukan pada permukaan cairan, misalnya karena perubahan tekanan atmosfer atau tekanan piston, mestilah merupakan penambahan tekanan pada semua titik dalam cairan, seperti dikemukakan oleh Blaise Pascal (1623-1662), yang dikenal sebagai Hukum Pascal.

Tekanan yang dilakukan pada cairan dalam ruang tertutup, akan diteruskan kemana-mana sama besarnya termasuk dinding tempatnya.

Apabila kerapatan ρ (massa jenis) sangat kecil, misalnya fluida berbentuk gas, maka perbedaan tekanan pada dua titik di dalam fluida dapat diabaikan. Jadi di dalam suatu bejana yang berisi gas, tekanan gas di mana-mana adalah sama. Hal ini tentu saja bukan untuk ∆h yang sangat besar. Tekanan dari udara sangat bervariasi untuk ketinggian yang besar dalam atmosfer. Dalam kenyataan, kerapatan ρ berbeda pada ketinggian yang tidak sama dan ρ ini hendaklah kita ketahui sebagai fungsi dari h sebelum persamaan 3 di atas kita pergunakan.

Marilah kita perhatikan hal berikut ini. Andaikan ke dalam pipa berbentuk U dimasukkan dua jenis cairan yang tidak dapat bercampur secara sempurna, misalnya air dengan minyak tanah.

Gambar 4. Pipa berbentuk U berisi dua jenis cairan.

Setelah cairan yang kerapatannya ρ₁ dimasukkan ke dalam pipa, cairan yang kedua dengan kerapatan ρ₂ (di mana ρ₁ > ρ₂) dimasukkan ke salah satu pipa sehingga permukaan cairan yang pertama turun setinggi 1 di bawah cairan yang kedua itu, sedangkan permukaan lainnya naik setinggi 1 seperti dilukiskan pada gambar 4 di atas. Akan kita tentukan perbandingan kerapatan kedua jenis cairan tersebut. Pada gambar 4 titik C menyatakan keseimbangan tekanan. Tekanan di C yang dilakukan cairan di atasnya adalah

Untuk cairan pertama : p₁ g 2 1

Untuk cairan kedua : p₁ g 2 1

Sehingga :

ρ₁ g 2 1 = ρ₂ g (d + 2 1)

atau

ρ₂ 2 1

=

ρ₁ d + 2 1

Perbandingan kerapatan suatu bahan terhadap kerapatan air dinamakan kerapatan relatif atau gravitas spesifik dari bahan tersebut.

Archimedes mendapatkan suatu prinsip sebagai berikut. Apabila suatu benda dicelupkan ke dalam cairan (seluruhnya atau sebagian), benda itu mengalami gaya ke atas sebesar berat cairan yang dipindahkannya.

Apabila sebuah benda dicelupkan ke dalam cairan, seperti ditunjukkan dalam gambar 5, total gaya ke atas atau gaya angkat, dilakukan pada benda. Akibat gaya ini terdapat perbedaan tekanan pada bagian bawah dan bagian atas benda. Selama tekanan ini tergantung pada kedalaman cairan, dengan mudah dapat kita hitung gaya ke atas untuk sederhana, antara lain untuk balok tegar di mana salah satu permukaannya horizontal.

Gambar 5. Gaya-gaya yang dialami benda di dalam cairan.

Benda yang bentuknya sembarang, agak sulit kita menentukan tekanan karena bervariasinya titik-titik permukaan benda. Untuk itu prinsip Archimedes sangat membantu. Andaikan benda dikeluarkan dari dalam cairan akan menggantikan tempat benda sebanyak tempat yang tadinya ditempati oleh benda. Jika volume tempat benda itu telah diisi oleh cairan, ini menunjukkan bahwa adanya keseimbangan gaya yang terjadi antar cairan penyelubung dengan bagian cairan yang menggantikan tempat benda tersebut. Jadi gaya netto yang arahnya ke atas adalah sama dengan m₁ g, di mana m₁ adalah massa cairan yang mengisi volume yang ditinggalkan oleh benda.

Sekarang kita tinggalkan pengandaian tadi dengan benda sesungguhnya yang massanya m_o. Cairan mestilah melakukan kontak dengan setiap titik pada permukaan benda yang memberikan gaya-gaya sama di mana-mana. Gaya ini mestilah sama dengan gaya penopang cairan yang volumenya adalah sama. Gaya ini adalah gaya angkat (ke atas) yang besar.

F_b = m_f g = ρ₁ V_g (5)

Di mana m₁ adalah massa cairan yang dipindahkan oleh benda yang tercelup ke dalam cairan adalah kerapatan cairan. Gaya angkat ini arahnya vertikal ke atas.

Persamaan 5 dinamakan Prinsip Archimedes yang dikemukakan oleh Archimedes pada tahun 250 SM. Jika gaya ke atas lebih kecil daripada berat benda yang dicelupkan, mala benda itu akan tenggelam. Jika berat benda lebih kecil daripada gaya ke atas, benda itu akan terapung. Seandainya ρ_o adalah kerapatan benda, dengan volume V, maka beratnya

W = m_o g = ρ_o V g

Gaya ke atas dinyatakan oleh persamaan 5.

F_b = ρ1 V g (6)

Netto gaya ke atas ketika benda semuanya tercelup dalam cairan

F_net = F_b . W =( ρ_f. ρ_o) V g (7)

Jadi benda dengan kerapatan lebih besar dari kerapatan cairan akan tenggelam, dan yang lebih kecil akan terapung.

Sekarang Anda lakukan latihan sebagai berikut.

1. Sebuah balon terbuat dari karet massanya 2 g diisi dengan gas helium yang massanya ¾ g. JIka volume balon itu 41, akan kita cari gaya ke atas netto yang bekerja pada balon.

2. Balok kayu yang kerapatannya 0,6 cm^-3 berupa kubus dengan rusuk 10 cm terapung di dalam air seperti dilukiskan pada gambar 6. Akan kita tentukan bagian kayu yang tidak tercelup dalam air.

Fluida adalah sub-himpunan dari fase benda, termasuk cairan, gas, plasma, dan padat plastik

Fluida adalah zat yang dapat mengalami perubahan bentuk secara kontinu bila terkena tegangan geser walaupun relatif kecil. Gaya geser adalah komponen gaya yang menyinggung permukaan dan jika dibagi dengan luas permukaan tersebut menjadi tegangan geser rata-rata pada permukaan itu.

Fluida memilik sifat tidak menolak terhadap perubahan bentuk dan kemampuan untuk mengalir (atau umumnya kemampuannya untuk mengambil bentuk dari wadah mereka). Sifat ini biasanya dikarenakan sebuah fungsi dari ketidakmampuan mereka mengadakan tegangan geser(shear stress) dalam ekuilibrium statik. Konsekuensi dari sifat ini adalah hukum Pascaltekanan dalam mengkarakterisasi bentuk fluid. Dapat disimpulkan bahwa fluida adalah zat atau entitas yang terdeformasi secara berkesinambungan apabila diberi tegangan geser walau sekecil apapun tegangan geser itu. yang menekankan pentingnya

Fluid dapat dikarakterisasikan sebagai:

• Fluida Newtonian
• Fluida Non-Newtonian

Fluida juga dibagi menjadi cairan dan gas. Cairan membentuk permukaan bebas yaitu: permukaan yang tidak diciptakan oleh bentuk wadahnya), sedangkan gas tidak.

Tekanan dalam Fluida

Konsep Tekanan pada Fluida

Dalam ilmu fisika, Tekanan diartikan sebagai gaya per satuan luas, di mana arah gaya tegak lurus dengan luas permukaan. Secara matematis, tekanan dapat dinyatakan dengan persamaan berikut ini :

P = tekanan (N)
F = gaya dan
A = luas permukaan (m²).

Karena tekanan adalah gaya per satuan luas maka satuan tekanan adalah N/m ². Nama lain dari N/m² adalah pascal (Pa). Pascal dipakai sebagai satuan Tekanan untuk menghormati om Blaise Pascal. Kita akan berkenalan lebih dalam dengan om Pascal pada pokok bahasan Prinsip Pascal.

Misalkan kita sedang berendam di dalam air, apa yang kita rasakan? Seolah-olah air menekan seluruh tubuh kita yang bersentuhan dengan air. Tekanan ini semakin besar apabila kita masuk lebih dalam ke dalam air. Fenomena apa yang ada dibalik peristiwa ini?

Pernyataan ini mengandung pengertian bahwa fluida memberikan tekanan terhadap benda yang berada di dalamnya. Pengertian ini diperluas menjadi tekanan pada fluida tergantung pada ketebalannya atau lebih tepatnya kedalamannya.

Udara/atmosfer terdiri dari gas-gas yang juga merupakan bentuk dari fluida. Maka udara juga akan memiliki tekanan seperti definisi di atas. Tekanan udara kita anggap sama untuk ketinggian tertentu di atas bumi namun untuk ketinggian yang sangat tinggi di atas permukaan bumi besarnya menjadi berbeda. Hal ini dapat dilakukan karena udara kita anggap kerapatannya kecil sehingga untuk titik-titik yang tidak terlalu jauh perbedaan ketinggiannya bisa dianggap sama.

Suatu zat yang mempunyai kemampuan mengalir dinamakan fluida. Cairan adalah salah satu jenis fluida yang mempunyai kerapatan mendekati zat padat. Letak partikelnya lebih merenggang karena gaya interaksi antar partikelnya lemah. Gas juga merupakan fluida yang interaksi antar partikelnya sangat lemah sehingga diabaikan. Dengan demikian kerapatannya akan lebih kecil. Karena itu, fluida dapat ditinjau sebagai sistem partikel dan kita dapat menelaah sifatnya dengan menggunakan konsep mekanika partikel. Apabila fluida mengalami gaya geser maka akan siap untuk mengalir. Jika kita mengamati fluida statik, misalnya air di tempayan. Sistem ini tidak mengalami gaya geser tetapi mempunyai tekanan pada dinding tempayan.

Momen Inersia

Momen inersia (satuan SI kg m²) adalah ukuran ketahanan objek terhadap perubahan laju rotasinya. Besaran ini adalah analog rotasi daripada massa. Dengan kata lain, besaran ini adalah kelembaman sebuah benda tegar yang berputar terhadap rotasinya. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.

Lambang I dan kadang-kadang juga J biasanya digunakan untuk merujuk kepada momen inersia.

Konsep ini diperkenalkan oleh Euler dalam bukunya a Theoria motus corporum solidorum seu rigidorum pada tahun 1730.^[1] Dalam buku tersebut, dia mengupas momen inersia dan banyak konsep terkait.

Definisi skalar

Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) dari sembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:

di mana m adalah massa dan r adalah jarak tegak lurus terhadap sumbu rotasi.

Analisis

Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh

Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik m_i dengan jarak r_i terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:

Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:

di mana

V adalah volume yang ditempati objek

ρ adalah fungsi kerapatan spasial objek

r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut.

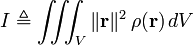
Diagram perhitungan momen inersia sebuah piringan. Di sini k adalah 1/2 dan adalah jari-jari yang digunakan untuk menentukan momen inersia

Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk:

di mana

M adalah massa

R adalah jari-jari objek dari pusat massa (dalam beberapa kasus, panjang objek yang digunakan)

k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yang berbeda-beda tergantung pada objek terkait.

Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. Contoh:

• k = 1, cincin tipis atau silinder tipis di sekeliling pusat
• k = 2/5, bola pejal di sekitar pusat
• k = 1/2, silinder atau piringan pejal di sekitar pusat.

Cincin tipis berjari-jari R,

bermassa M dan lebar L (sumbu rotasi terletak di tengah-tengah salah satu diameter)

Cincin tipis berjari-jari R, bermassa M dan lebar L

(sumbu rotasi terletak pada salah satu garis singgung)

Silinder berongga,

dengan jari-jari dalam R₂ dan jari-jari luar R₁

Silinder padat

dengan jari-jari R (sumbu rotasi terletak pada sumbu silinder)

Silinder padat dengan jari-jari R

(sumbu rotasi terletak pada diameter pusat)

Bola pejal dengan jari-jari R

(sumbu rotasi terletak pada salah satu diameter)

Kulit Bola dengan jari-jari R

(sumbu rotasi terletak pada salah satu diameter)

Batang pejal yang panjangnya L

(sumbu rotasi terletak pada pusat )

Batang pejal yang panjangnya L

(sumbu rotasi terletak pada salah satu ujung)

Balok pejal yang panjangnya P dan lebarnya L

(sumbu rotasi terletak pada pusat; tegak lurus permukaan)

Latihan Soal 1 :

Sebuah partikel bermassa 2 kg diikatkan pada seutas tali yang panjangnya 0,5 meter (lihat gambar di bawah). Berapa momen Inersia partikel tersebut jika diputar ?

Panduan Jawaban :

Catatan :

Yang kita bahas ini adalah rotasi partikel, bukan benda tegar. Jadi bisa dianggap massa benda terkonsentrasi pada pusat massanya.

Momen inersianya berapa-kah ?

I = mr²

I = (2 kg) (0,5m)²

I = 0,5 kg m²

Gampang…..

Latihan Soal 2 :

Dua partikel, masing-masing bermassa 2 kg dan 4 kg, dihubungkan dengan sebuah kayu yang sangat ringan, di mana panjang kayu = 2 meter. (lihat gambar di bawah). Jika massa kayu diabaikan, tentukan momen inersia kedua partikel itu, jika :

a) Sumbu rotasi terletak di antara kedua partikel

Panduan Jawaban :

Momen inersia = 6 kg m²

b) Sumbu rotasi berada pada jarak 0,5 meter dari partikel yang bermassa 2 kg

Momen inersia = 9,5 kg m²

c) Sumbu rotasi berada pada jarak 0,5 meter dari partikel yang bermassa 4 kg

Momen inersia = 5,5 kg m²

Berdasarkan hasil perhitungan di atas, tampak bahwa Momen Inersia sangat dipengaruhi oleh posisi sumbu rotasi. Hasil oprekan soal menunjukkan hasil momen Inersia yang berbeda-beda. Partikel yang berada di dekat sumbu rotasi memiliki momen inersia yang kecil, sebaliknya partikel yang berada jauh dari sumbu rotasi memiliki momen inersia yang besar. Jika kita mengandaikan bahwa kedua partikel di atas merupakan benda tegar, maka setiap partikel penyusun benda tegar yang berada di dekat sumbu rotasi memiliki momen inersia yang lebih kecil dibandingkan dengan momen inersia partikel yang jaraknya lebih jauh dari sumbu rotasi. Walaupun bentuk dan ukuran sama, tapi karena posisi sumbu rotasi berbeda, maka momen inersia juga berbeda.

Latihan Soal 3 :

Empat partikel, masing-masing bermassa 2 kg dihubungkan oleh batang kayu yang sangat ringan dan membentuk segiempat (lihat gambar di bawah). Tentukan momen inersia gabungan keempat partikel ini, jika mereka berotasi terhadap sumbu seperti yang ditunjukkan pada gambar (massa kayu diabaikan).

Momen iInersia gabungan dari keempat partikel ini (dianggap satu sistem) mudah dihitung. Jarak masing-masing partikel dari sumbu rotasi sama (r_A = r_B = r_C = r_D = 1 meter). Jarak AC = BD = 4 meter tidak berpengaruh, karena yang diperhitungkan hanya jarak partikel diukur dari sumbu rotasi.

I = mr²

I = (2 kg)(1 m)²

I = 2 kg m²

Karena I_A = I_B = I_C = I_D = I, maka momen inersia (I) total :

I = 4(I)

I = 4(2 kg m²)

I = 8 kg m²