Momen inersia (satuan SI kg m2) adalah ukuran ketahanan objek terhadap perubahan laju rotasinya. Besaran ini adalah analog rotasi daripada massa. Dengan kata lain, besaran ini adalah kelembaman sebuah benda tegar yang berputar terhadap rotasinya. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.
Lambang I dan kadang-kadang juga J biasanya digunakan untuk merujuk kepada momen inersia.
Konsep ini diperkenalkan oleh Euler dalam bukunya a Theoria motus corporum solidorum seu rigidorum pada tahun 1730.[1] Dalam buku tersebut, dia mengupas momen inersia dan banyak konsep terkait.
Definisi skalar
Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) dari sembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:
di mana m adalah massa dan r adalah jarak tegak lurus terhadap sumbu rotasi.
Analisis
Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh
Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik mi dengan jarak ri terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:
Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:
di mana
- V adalah volume yang ditempati objek
- ρ adalah fungsi kerapatan spasial objek
- r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut.
Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk:
di mana
- M adalah massa
- R adalah jari-jari objek dari pusat massa (dalam beberapa kasus, panjang objek yang digunakan)
- k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yang berbeda-beda tergantung pada objek terkait.
Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. Contoh:
- k = 1, cincin tipis atau silinder tipis di sekeliling pusat
- k = 2/5, bola pejal di sekitar pusat
- k = 1/2, silinder atau piringan pejal di sekitar pusat.
Cincin tipis berjari-jari R,
bermassa M dan lebar L (sumbu rotasi terletak di tengah-tengah salah satu diameter)
![]()

Cincin tipis berjari-jari R, bermassa M dan lebar L
(sumbu rotasi terletak pada salah satu garis singgung)
![]()

Silinder berongga,
dengan jari-jari dalam R2 dan jari-jari luar R1
![]()

Silinder padat
dengan jari-jari R (sumbu rotasi terletak pada sumbu silinder)
![]()

Silinder padat dengan jari-jari R
(sumbu rotasi terletak pada diameter pusat)
![]()

Bola pejal dengan jari-jari R
(sumbu rotasi terletak pada salah satu diameter)
![]()

Kulit Bola dengan jari-jari R
(sumbu rotasi terletak pada salah satu diameter)
![]()

Batang pejal yang panjangnya L
(sumbu rotasi terletak pada pusat )
![]()

Batang pejal yang panjangnya L
(sumbu rotasi terletak pada salah satu ujung)
![]()

Balok pejal yang panjangnya P dan lebarnya L
(sumbu rotasi terletak pada pusat; tegak lurus permukaan)
![]()

Latihan Soal 1 :
Sebuah partikel bermassa 2 kg diikatkan pada seutas tali yang panjangnya 0,5 meter (lihat gambar di bawah). Berapa momen Inersia partikel tersebut jika diputar ?

Panduan Jawaban :
Catatan :
Yang kita bahas ini adalah rotasi partikel, bukan benda tegar. Jadi bisa dianggap massa benda terkonsentrasi pada pusat massanya.
Momen inersianya berapa-kah ?
I = mr2
I = (2 kg) (0,5m)2
I = 0,5 kg m2
Gampang…..
Latihan Soal 2 :
Dua partikel, masing-masing bermassa 2 kg dan 4 kg, dihubungkan dengan sebuah kayu yang sangat ringan, di mana panjang kayu = 2 meter. (lihat gambar di bawah). Jika massa kayu diabaikan, tentukan momen inersia kedua partikel itu, jika :
a) Sumbu rotasi terletak di antara kedua partikel

Panduan Jawaban :


Momen inersia = 6 kg m2
b) Sumbu rotasi berada pada jarak 0,5 meter dari partikel yang bermassa 2 kg


Momen inersia = 9,5 kg m2
c) Sumbu rotasi berada pada jarak 0,5 meter dari partikel yang bermassa 4 kg


Momen inersia = 5,5 kg m2
Berdasarkan hasil perhitungan di atas, tampak bahwa Momen Inersia sangat dipengaruhi oleh posisi sumbu rotasi. Hasil oprekan soal menunjukkan hasil momen Inersia yang berbeda-beda. Partikel yang berada di dekat sumbu rotasi memiliki momen inersia yang kecil, sebaliknya partikel yang berada jauh dari sumbu rotasi memiliki momen inersia yang besar. Jika kita mengandaikan bahwa kedua partikel di atas merupakan benda tegar, maka setiap partikel penyusun benda tegar yang berada di dekat sumbu rotasi memiliki momen inersia yang lebih kecil dibandingkan dengan momen inersia partikel yang jaraknya lebih jauh dari sumbu rotasi. Walaupun bentuk dan ukuran sama, tapi karena posisi sumbu rotasi berbeda, maka momen inersia juga berbeda.
Latihan Soal 3 :
Empat partikel, masing-masing bermassa 2 kg dihubungkan oleh batang kayu yang sangat ringan dan membentuk segiempat (lihat gambar di bawah). Tentukan momen inersia gabungan keempat partikel ini, jika mereka berotasi terhadap sumbu seperti yang ditunjukkan pada gambar (massa kayu diabaikan).

Momen iInersia gabungan dari keempat partikel ini (dianggap satu sistem) mudah dihitung. Jarak masing-masing partikel dari sumbu rotasi sama (rA = rB = rC = rD = 1 meter). Jarak AC = BD = 4 meter tidak berpengaruh, karena yang diperhitungkan hanya jarak partikel diukur dari sumbu rotasi.
I = mr2
I = (2 kg)(1 m)2
I = 2 kg m2
Karena IA = IB = IC = ID = I, maka momen inersia (I) total :
I = 4(I)
I = 4(2 kg m2)
I = 8 kg m2



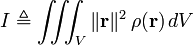

 adalah jari-jari yang digunakan untuk menentukan momen inersia
adalah jari-jari yang digunakan untuk menentukan momen inersia

Tidak ada komentar:
Posting Komentar