keseimbangan benda tegar: Titik Berat

TITIK BERAT

Setiap partikel dalam suatu benda memiliki berat. Berat seluruh benda adalah resultan dari semua gaya gravitasi berarah vertikal ke bawah dari semua partikel ini. Rersultan ini bekerja melalui suatu titik tunggal, yang disebut titik berat (Pusat gravitasi)
Koordinat titik berat dapat dihitung dengan rumus sbb :

Bila benda berada pada medan gravitasi yang homogen, maka persamaan tersebut dapat ditulis menjadi :

Untuk benda dalam satu dimensi rumus diatas dapat ditulis menjadi :

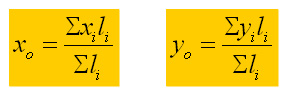Untuk benda dalam dua dimensi rumus diatas dapat ditulis menjadi :

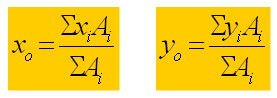Untuk benda dalam tiga dimensi rumus diatas dapat ditulis menjadi :

Untuk benda-benda yang bentuknya simetris letak titik beratnya dapat dilihat pada tabel berikut :

ROTASI BENDA TEGAR

Hukum dasar mekanika terbukti mampu menjelaskan berbagai fenomena yang berhubungan dengan sistem diskrit (partikel). Hukum dasar ini tercakup dalam formulasi Hukum Newton tentang gerak. Selain sistem diskrit di alam ini terdapat bentuk sistem lain yaitu sistem kontinyu yang mencakup benda tegar dan fluida. Pada bagian ini akan dibahas formulasi hukum mekanika pada benda tegar yang pada akhirnya akan diperoleh bahwa hukum-hukum yang berlaku pada sistem diskrit juga berlaku pada sistem kontinu ini.

Perbedaan mendasar antara partikel dan benda tegar adalah bahwa suatu partikel hanya dapat mengalami gerak translasi (gerak lurus) saja, sedangkan benda tegar selain dapat mengalami gerak translasi juga dapat bergerak rotasi yaitu gerak mengelilingi suatu poros. Berbagai aspek dari gerak rotasi inilah yang akan menjadi pokok pembahasan pada bab ini.

Baik fluida yang merupakan materi dalam wujud gas atau cair sangat berbeda dengan partikel maupun benda tegar yang berwujud padat, keduanya memiliki hukum dasar yang sama, yaitu hukum dasar mekanika.

Rotasi Benda Tegar : Torsi

Pengamatan terhadap alam di sekitar kita menunjukan kepada kita salah satu bentuk gerak berupa gerak berputar pada porosnya. Jenis gerak ini dinamakan gerak rotasi. Gerak bumi pada porosnya adalah salah satu contoh dari gerak rotasi. Gerak rotasi bumi memungkinkan terjadinya siang dan malam. Ketika kita membuka dan menutup pintu rumah kita, dorongan tangan kita menimbulkan gerak rotasi pintu terhadap engselnya.

Sekarang mari kita tinjau sebuah pintu. Apabila kita mendorong pintu tersebut, maka pintu akan berputar sesuai dengan arah dorongan gaya yang diberikan. Gaya dorong yang menyebabkan pintu berputar selalu berjarak tertentu dari poros putaran. Apabila kita beri gaya dorong tepat di poros, niscaya pintu itu tidak akan berputar. Jarak poros putaran dengan letak gaya dinamakan lengan momen.

Jadi, bisa dikatakan perkalian gaya dan lengan momen ini yang menyebabkan benda berputar. Besaran ini dinamakan torsi atau momen gaya.

Pengertian torsi dalam gerak rotasi serupa dengan gaya pada gerak translasi yaitu sebagai penyebab terjadinya gerak. Menurut hukum Newton, benda bergerak disebabkan oleh gaya. Prinsip ini juga berlaku pada gerak rotasi yang berarti benda bergerak rotasi disebabkan oleh torsi.

Kita bisa mendefinisikan suatu besaran baru, yaitu momen inersia yang menyatakan kelembaman benda ketika benda bergerak rotasi. Momen inersia analogi dengan massa pada gerak translasi.

Torsi atau momen gaya juga dihasilkan dari momen inersia dikalikan dengan percepatan rotasi (percepatan sudut). Ini merupakan analogi dari gaya sama dengan massa dikali percepatan yang merupakan bentuk hukum Newton kedua. Jadi, hukum Newton kedua juga berlaku dalam gerak rotasi. Penjelasan di atas mengungkapkan berlakunya hukum Newton pada gerak rotasi.

titik berat

Telah dikatakan sebelumnya bahwa suatu benda tegar dapat mengalami gerak translasi (gerak lurus) dan gerak rotasi. Benda tegar akan melakukan gerak translasi apabila gaya yang diberikan pada benda tepat mengenai suatu titik yang yang disebut titik berat.

Benda akan seimbang jika pas diletakkan di titik beratnya

Titik berat merupakan titik dimana benda akan berada dalam keseimbangan rotasi (tidak mengalami rotasi). Pada saat benda tegar mengalami gerak translasi dan rotasi sekaligus, maka pada saat itu titik berat akan bertindak sebagai sumbu rotasi dan lintasan gerak dari titik berat ini menggambarkan lintasan gerak translasinya.

Mari kita tinjau suatu benda tegar, misalnya tongkat pemukul kasti, kemudian kita lempar sambil sedikit berputar. Kalau kita perhatikan secara aeksama, gerakan tongkat pemukul tadi dapat kita gambarkan seperti membentuk suatu lintasan dari gerak translasi yang sedang dijalani dimana pada kasus ini lintasannya berbentuk parabola. Tongkat ini memang berputar pada porosnya, yaitu tepat di titik beratnya. Dan, secara keseluruhan benda bergerak dalam lintasan parabola. Lintasan ini merupakan lintasan dari posisi titik berat benda tersebut.

Demikian halnya seorang peloncat indah yang sedang terjun ke kolam renang. Dia melakukan gerak berputar saat terjun. sebagaimana tongkat pada contoh di atas, peloncat indah itu juga menjalani gerak parabola yang bisa dilihat dari lintasan titik beratnya. Perhatikan gambar berikut ini.

seorang yang meloncat ke air dengan berputar

Jadi, lintasan gerak translasi dari benda tegar dapat ditinjau sebagai lintasan dari letak titik berat benda tersebut. Dari peristiwa ini tampak bahwa peranan titik berat begitu penting dalam menggambarkan gerak benda tegar.

Cara untuk mengetahui letak titik berat suatu benda tegar akan menjadi mudah untuk benda-benda yang memiliki simetri tertentu, misalnya segitiga, kubus, balok, bujur sangkar, bola dan lain-lain. Yaitu d sama dengan letak sumbu simetrinya. Hal ini jelas terlihat pada contoh diatas bahwa letak titik berat sama dengan sumbu rotasi yang tidak lain adalah sumbu simetrinya.

Orang ini berada dalam keseimbangan

Di sisi lain untuk benda-benda yang mempunyai bentuk sembarang letak titik berat dicari dengan perhitungan. Perhitungan didasarkan pada asumsi bahwa kita dapat mengambil beberapa titik dari benda yang ingin dihitung titik beratnya dikalikan dengan berat di masing-masing titik kemudian dijumlahkan dan dibagi dengan jumlah berat pada tiap-tiap titik. dikatakan titik berat juga merupakan pusat massa di dekat permukaan bumi, namun untuk tempat yang ketinggiannya tertentu di atas bumi titik berat dan pusat massa harus dibedakan.